When to Use Contextual Bandits: The Decision Framework
Part 1 of 5: Understanding the Landscape
TL;DR: Contextual bandits bridge the gap between static A/B testing and full reinforcement learning. Use them when you need personalized, adaptive optimization with immediate feedback—but not for sequential decision-making or when you need clean causal inference. This post helps you decide if bandits are right for your problem.
Reading time: ~20 minutes
The Adaptive Optimization Gap
You’re running an A/B test to optimize your recommendation system. Variant A gets 50% of traffic, variant B gets 50%. You wait three weeks for statistical significance. Finally, results are in: B wins with 5.2% lift. You ship it to 100% of users.
But here’s what you missed: During those three weeks, 50% of your users got the inferior experience. And variant B might work great for power users but poorly for newcomers—your aggregate metric doesn’t capture this. You just left significant value on the table.
This is the adaptive optimization gap that contextual bandits solve.
The contextual bandit loop
Before diving deeper, understand the core interaction pattern:
The key difference from A/B testing: Step 4 happens immediately after each interaction. The policy learns and adapts continuously, not after weeks of fixed allocation.
Quick Start: Is This Guide For You?
✅ This series is for you if:
- You’re optimizing recommendations, rankings, or content selection
- You have >1000 decisions/day with measurable outcomes
- User preferences vary (personalization matters)
- You need faster learning than A/B testing provides
❌ Skip to alternatives if:
- Decisions are highly sequential (use RL instead)
- Feedback is delayed >1 week (use delayed RL)
- You have <100 decisions/day (use A/B testing)
- Context doesn’t matter (use multi-armed bandit)
What Are Contextual Bandits?
Starting Simple: The Casino Analogy
Multi-Armed Bandit (MAB): You walk into a casino with K slot machines. Each has an unknown payout rate. Your goal: maximize winnings over 1000 plays.
The challenge: explore (try machines to learn rates) vs. exploit (play the best one). Every player faces the same problem—machine 3 is either best for everyone or no one. No personalization.
The Real World Problem: The “best” choice depends on who you are and the situation.
News articles example: {Tech, Sports, Politics}
- MAB thinking: “Sports gets 15% CTR on average → show Sports to everyone”
- Reality: Tech enthusiasts click Tech 40% vs Sports 5%. Sports fans reverse this pattern.
- The insight: Optimal action changes based on context (user type).
Technical Definition
Contextual Bandit: An online learning algorithm for personalized decision-making under uncertainty.
Mathematical Formulation:
At each timestep t = 1, 2, …, T:
- Observe context Context vector with d features (user demographics, item attributes, environment)
- Choose action Select from K available actions based on context
- Receive reward Observe stochastic reward from unknown distribution
- Update model Learn to predict expected reward for any (context, action) pair
- Repeat with continuous adaptation
Goal: Learn policy that maximizes cumulative reward:
Key Differences from MAB:
| Aspect | Multi-Armed Bandit | Contextual Bandit |
|---|---|---|
| Learning task | K numbers: | Function: |
| Personalization | None (global optimum) | Per-context optimization |
| Complexity | Simple | Moderate (function approximation) |
| Sample efficiency | Good for homogeneous | Better for heterogeneous |
Concrete Example: Content Recommendation
Setup:
Context x ∈ ℝ⁵:
x = [user_age, user_tenure_days, is_mobile, time_of_day, topic_affinity]
Example: x₁ = [28, 450, 1, 14, 0.8]
(28yo, 450 days tenure, mobile, 2pm, 80% tech affinity)
Actions a ∈ {1, 2, 3}:
a=1: article_A (tech content)
a=2: article_B (sports content)
a=3: article_C (politics content)
Reward r ∈ {0, 1}:
r = 1 if user clicks, r = 0 otherwise
How MAB Fails:
After 1000 uniform trials:
article_A: 120/333 = 36% CTR
article_B: 133/333 = 40% CTR ← Highest average
article_C: 97/334 = 29% CTR
MAB decision: Always show article_B
Problem: Misses that tech users prefer A, sports fans prefer B
How Contextual Bandit Succeeds:
Learn function :
Tech enthusiast: x₁ = [28, 450, 1, 14, 0.8]
f(x₁, article_A) = 0.75 ← Optimal for this user
f(x₁, article_B) = 0.15
f(x₁, article_C) = 0.10
→ Recommend article_A
Sports fan: x₂ = [45, 1200, 0, 19, 0.2]
f(x₂, article_A) = 0.12
f(x₂, article_B) = 0.68 ← Optimal for this user
f(x₂, article_C) = 0.20
→ Recommend article_B
Result: Personalized CTR ~55% vs MAB’s global 40%.
The Learning Challenge
What makes this hard:
- Partial feedback: Only observe reward for chosen action
- Chose A, saw reward 1 → What would B have given? Unknown (counterfactual)
- Must explore alternatives to learn their value
- Function approximation: Learning across continuous context space
- Can’t try every possible x (infinite contexts)
- Must generalize from observed data to unseen contexts
- Exploration-exploitation tradeoff:
- Explore: Try uncertain actions to gather information (short-term cost)
- Exploit: Choose known best action to maximize reward (long-term requires learning)
- Balance: Neither pure exploration nor pure exploitation is optimal
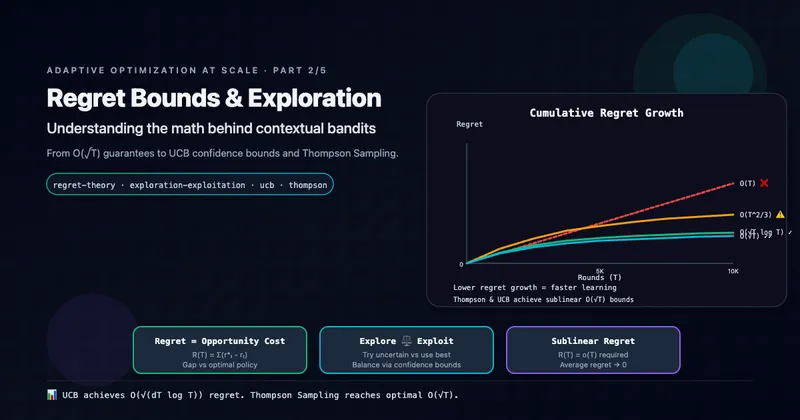
Optimal algorithms (LinUCB, Thompson Sampling) achieve regret—near-optimal convergence to best policy.
Where Contextual Bandits Fit
| Method | Context? | Online Learning? | Explores? | Use Case |
|---|---|---|---|---|
| A/B Test | ❌ | ❌ | Yes (forced) | One-time experiments |
| Supervised ML | ✅ | ❌ | ❌ | Offline labeled data |
| MAB | ❌ | ✅ | ✅ | Homogeneous population |
| Contextual Bandit | ✅ | ✅ | ✅ | Personalized + adaptive |
| Full RL | ✅ | ✅ | ✅ | Sequential decisions |
Critical distinction from RL:
Contextual bandits are stateless. Each decision is independent.
Contextual Bandit (memoryless):
t=1: x₁ → a₁ → r₁
t=2: x₂ → a₂ → r₂ (x₂ independent of a₁)
Full RL (stateful):
t=1: s₁ → a₁ → r₁ → s₂
t=2: s₂ → a₂ → r₂ → s₃ (s₂ caused by a₁)
Example: Recommending an article doesn’t change tomorrow’s user → bandit. Playing chess (moves change board state) → RL.
Why Contextual Bandits Matter
1. Automatic Personalization
Traditional:
Run A/B test → Analyst finds "B wins for 18-25, A for 40+"
→ Engineer 2-variant system → Repeat for each feature
Contextual bandit:
Deploy with features → Learns f(age, location, ...) → best action
→ Discovers "A wins for 18-25 + mobile + evening" automatically
2. Sample Efficiency
Over 10,000 decisions:
- A/B test (50/50 split): ~5,000 suboptimal → 2,500 lost conversions
- Contextual bandit: ~500 exploratory → 100 lost conversions
- Savings: 2,400 conversions (48% improvement)
3. Continuous Adaptation
Handles non-stationarity:
- User preferences shift (trends)
- Seasonality (December ≠ July)
- Competition (dynamic pricing)
- External shocks (COVID)
Bandit automatically detects changes and adapts. A/B test remains static until next experiment.
Real-world impact:
- Netflix: 20-30% engagement lift (personalized artwork)
- E-commerce: 5-15% revenue increase (dynamic pricing)
- Healthcare: 10-25% outcome improvement (treatment personalization)
Quick Decision Guide
✅ Use contextual bandits when:
- Context predicts optimal action (heterogeneous users/situations)
- Decisions are independent (stateless)
- Feedback is immediate (seconds to days)
- Scale justifies complexity (1000+ decisions/day)
- Reward is measurable and well-defined
❌ Use alternatives when:
- No context → MAB
- Sequential dependencies → Full RL
- Delayed rewards (>1 week) → Delayed RL
- Need causal estimates → A/B testing
- Low scale (<100/day) → A/B testing
The Problem with Static Experimentation
A/B testing is the gold standard for causal inference, but has fundamental limitations for adaptive optimization:
Core Limitations
1. Fixed allocation wastes traffic 50/50 split for entire experiment. Bad variants get equal traffic until significance.
2. No personalization Aggregate metrics hide segment-level differences. Manual segmentation requires pre-defining groups and exponentially splits traffic.
3. Slow adaptation Wait weeks for statistical power. System doesn’t learn during experiment.
4. Sequential testing overhead Testing 5 variants requires either multiple rounds (slow) or 5-way split (massive sample size needed).
Reality: Production systems need faster, adaptive, personalized optimization.
Understanding the Decision-Making Spectrum
| Dimension | A/B Testing | MAB | Contextual Bandit | Full RL |
|---|---|---|---|---|
| Adaptation | None | Global | Personalized | Sequential |
| Context use | Post-hoc | None | Core feature | State |
| Feedback | Delayed (weeks) | Immediate | Immediate | Delayed + sequential |
| Sample efficiency | Low | Medium | High | Very low |
| Complexity | Simple | Simple | Moderate | High |
Contextual Bandit vs Multi-Armed Bandit
The distinction: Do you have side information about the decision context?
MAB: Learn global optimum. Same best action for everyone.
When MAB suffices:
- Homepage layout (users identical)
- Global search ranking (uniform population)
- Fixed-time promotions (time is only context)
Example MAB failure:
Notification timing for fitness app:
MAB: Learns 7 PM is optimal on average (60% prefer evening, 40% prefer morning)
→ Converges to 7 PM (majority wins)
→ 40% of users get suboptimal forever
Contextual bandit: Uses activity patterns
→ Morning people → 6 AM, evening people → 7 PM
→ Personalized optimal for all
When CB is necessary:
- Product recommendations (preferences vary by user)
- Ad selection (relevance is contextual)
- Content ranking (interests heterogeneous)
Critical question: Is personalization lift > complexity cost? If users homogeneous → MAB. If diverse → CB.
Contextual Bandit vs A/B Testing
The Fundamental Tradeoff
| Dimension | A/B Testing | Contextual Bandit |
|---|---|---|
| Causal clarity | ✅ High (randomization) | ⚠️ Moderate (needs careful analysis) |
| Sample efficiency | ❌ Low (fixed allocation) | ✅ High (adaptive) |
| Personalization | ❌ None (aggregate) | ✅ Automatic |
| Speed to optimal | ❌ Slow (weeks) | ✅ Fast (days) |
| Organizational fit | ✅ Mature | ⚠️ Requires ML culture |
When to Use Each
A/B testing:
- Irreversible platform decisions (pricing, core UX)
- Need clean causal estimates (reporting/legal)
- Testing hypotheses, not optimizing
- Lack ML infrastructure
- Abundant sample size
Contextual bandits:
- Optimizing recommendations/rankings at scale
- High user heterogeneity
- Quick iteration on many variants
- Significant opportunity cost
- ML engineering resources available
Hybrid approach:
- Week 1-2: A/B test (validate personalization beats baseline)
- Week 3+: Deploy bandit (continuous optimization)
- Periodic A/B audits (validate effectiveness)
Contextual Bandit vs Full Reinforcement Learning
The boundary: Do current actions affect future rewards beyond immediate impact?
Contextual Bandits
One-step decisions. Each round:
- Observe context xₜ
- Choose action aₜ
- Receive reward rₜ
- Episode ends (next context independent)
Valid when:
- Recommendations (showing A doesn’t prevent showing B later)
- Ad serving (A doesn’t change future ad inventory)
- Email timing (7 PM today doesn’t affect tomorrow’s options)
Full RL
Sequential decisions. Markov Decision Process:
- States sₜ, actions aₜ
- Transitions P(sₜ₊₁|sₜ, aₜ) ← Actions affect future states
- Learn policy π(s) maximizing discounted cumulative reward
Required when:
- Game playing (moves change board)
- Inventory management (purchases deplete stock)
- Dialogue systems (responses change conversation)
The MDP Structure Test
Ask: “If I choose action A, does that change future actions available or desirable?”
- No → Bandit (ad A doesn’t change ad inventory)
- Weakly → Borderline (recommendation A slightly shifts interests)
- Strongly → RL (chess move A fundamentally changes options)
Sample Complexity Comparison
Sample complexity answers: “How many interactions needed to learn a near-optimal policy?”
Different from regret (cumulative loss), it measures the learning time itself.
| Problem Type | Regret Bound | Sample Complexity | What You’re Learning |
|---|---|---|---|
| Multi-armed bandit | O(√T) | O(K log T / Δ²) | K numbers (mean rewards) |
| Contextual bandit | O(√(dT log T)) | O(d log T / Δ²) | d-dimensional function |
| Tabular MDP | O(√(|S||A|T)) | O(|S|²|A| / (1-γ)³Δ²) | |S|²|A| transitions |
Where these come from:
-
Δ² in denominator: From hypothesis testing (Hoeffding’s inequality). To distinguish options with gap Δ requires O(1/Δ²) samples. Smaller gaps need exponentially more data.
-
d factor (contextual): Linear regression in d dimensions needs O(d/ε²) samples to achieve accuracy ε. With gap Δ, setting ε ~ Δ gives O(d/Δ²).
-
|S|² (MDP): Must learn P(s’|s,a) for all state pairs. Need to visit each (s,a) multiple times and estimate |S| transition probabilities per pair = O(|S|²).
-
(1-γ)³ (MDP): Discount γ determines effective horizon 1/(1-γ). Longer horizons need more samples to propagate value information. Cube comes from value error + mixing time + Bellman error propagation.
Sources:
- MAB: Auer et al. (2002), Lai & Robbins (1985)
- Contextual: Li et al. (2010), Abbasi-Yadkori et al. (2011)
- MDP: Kakade (2003), Strehl & Littman (2008)
Concrete example (Δ = 0.1 gap, 10K decisions):
MAB with K=10 arms:
Sample complexity: 10 × log(10,000) / 0.1² ≈ 9,200 samples
Contextual with d=20 features:
Sample complexity: 20 × log(10,000) / 0.1² ≈ 18,400 samples
Tabular MDP with |S|=100 states, |A|=10, γ=0.9:
Sample complexity: 100² × 10 / (0.1)³ × 0.001 ≈ 10,000,000 samples
Why this matters: RL sample complexity is 100-1000× higher than contextual bandits for equivalent problems. This isn’t just theory—it explains why recommendation systems learn in days (bandits) while game AI needs millions of episodes (RL).
RL sample complexity explodes with state space size and planning horizon. For large state spaces or long horizons, you need millions of samples.
Real-World Application Domains
1. Recommendation Systems
Context: User demographics, history, session behavior, item attributes Actions: Which items to recommend Reward: Clicks, purchases, watch time
Example: Netflix artwork personalization
2. Online Advertising
Context: User profile, page content, ad attributes Actions: Which ad to display Reward: Clicks (CTR) or conversions (CPA)
Challenges: Delayed conversion, budget constraints, dynamic bids
3. Content Ranking
Context: User preferences, content recency, feed position Actions: Order of content items Reward: Engagement (clicks, dwell time, shares)
Example: LinkedIn feed ranking
4. Personalized Notifications
Context: User timezone, engagement history, content urgency Actions: Send time (discrete slots) Reward: Open rate, click-through
Challenges: Delayed feedback, notification fatigue
5. Clinical Trials
Context: Patient demographics, medical history, biomarkers Actions: Treatment assignment Reward: Health outcomes
Challenges: Safety constraints, small samples, delayed outcomes, ethics
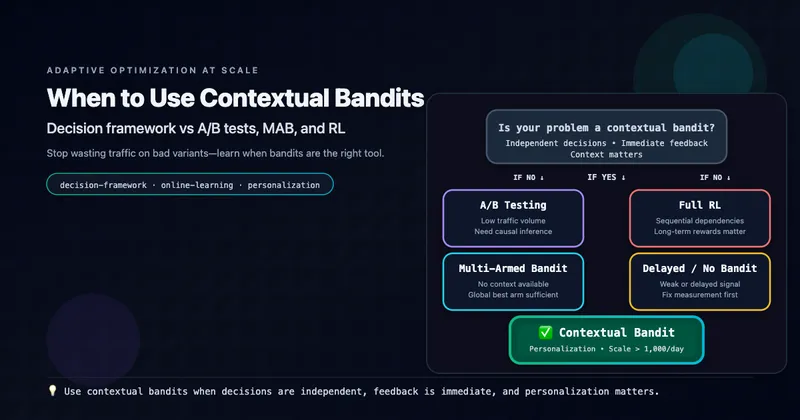
Decision Framework: Is Your Problem a Contextual Bandit?
✅ Requirements Checklist
- Independent decisions: Choices don’t affect future options/rewards
- Immediate feedback: Observe reward within seconds to days
- Heterogeneous contexts: Different situations favor different actions
- Multiple options: At least 2-3 actions to choose between
- Sufficient scale: 1000+ decisions/day for worthwhile learning
- Measurable reward: Clear metric capturing value
❌ Red Flags
- Sequential dependencies → Full RL
- Delayed feedback (>1 week) → Delayed RL
- Homogeneous population → MAB
- Only 1-2 total decisions → A/B testing
- Ambiguous reward → Fix measurement first
Decision Tree
Key Takeaways
Use contextual bandits when:
- Decisions independent (today doesn’t constrain tomorrow)
- Feedback immediate (seconds to days)
- Personalization matters (users/contexts differ)
- Scale sufficient (1000+ decisions/day)
Choose alternatives when:
- A/B testing: Need causal inference, low traffic, risk-averse
- MAB: Homogeneous population
- Full RL: Sequential dependencies, long horizons
Fundamental tradeoffs:
- A/B: Clean inference ↔ Sample efficiency
- Bandits: Adaptation ↔ Biased data
- RL: Sequential planning ↔ Sample complexity
Quick validation: ✅ Independent? ✅ Immediate? ✅ Heterogeneous? ✅ Multiple options? ✅ Scale? ✅ Measurable?
All ✅ → Contextual bandit likely right choice
Further Reading
Alternatives:
- A/B Testing: Trustworthy Online Controlled Experiments (Kohavi et al.)
- MAB: Introduction to Multi-Armed Bandits (Lattimore & Szepesvári)
- RL: Sutton & Barto’s RL Book
Contextual bandits:
- LinUCB paper (Li et al., 2010)
- Lil’Log: Multi-Armed Bandits
Production:
Article series
Adaptive Optimization at Scale: Contextual Bandits from Theory to Production
- Part 1 When to Use Contextual Bandits: The Decision Framework
- Part 2 Contextual Bandit Theory: Regret Bounds and Exploration
- Part 3 Implementing Contextual Bandits: Complete Algorithm Guide
- Part 4 Neural Contextual Bandits for High-Dimensional Data
- Part 5 Deploying Contextual Bandits: Production Guide and Offline Evaluation