LoRA and DoRA Implementation from Scratch


Goal
Implement Low-Rank Adaptation (LoRA) and Weight-Decomposed Low-Rank Adaptation (DoRA) layers from scratch in PyTorch, applied to Multi-Layer Perceptron models. This project helps understand the internals of parameter-efficient fine-tuning (PEFT) techniques that have become essential for adapting large language models.
Why Parameter-Efficient Fine-Tuning?
Fine-tuning large language models with billions of parameters is computationally expensive and requires significant memory. Parameter-efficient fine-tuning techniques address this by updating only a small subset of parameters while keeping the pretrained weights frozen.
Key benefits:
- Reduced memory footprint during training
- Faster training iterations
- Lower risk of catastrophic forgetting
- Ability to maintain multiple task-specific adaptations
LoRA: Low-Rank Adaptation
The Core Idea
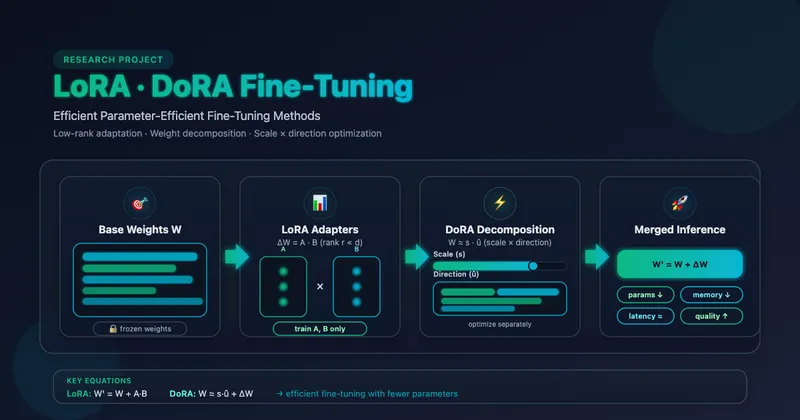
LoRA introduces trainable low-rank matrices alongside frozen pretrained weights. Instead of updating the full weight matrix W, we learn a low-rank decomposition that captures the task-specific adaptations.
Mathematical Formulation
For a pretrained weight matrix W₀ ∈ ℝᵈˣᵏ, LoRA modifies the forward pass as:
h = W₀x + ΔWx = W₀x + BAx
Where:
B ∈ ℝᵈˣʳandA ∈ ℝʳˣᵏare the low-rank matricesr << min(d, k)is the rank (typically 4, 8, or 16)- Only
AandBare trained;W₀remains frozen
The effective weight update becomes:
W' = W₀ + α · B · A
Where α is a scaling factor that controls the magnitude of the adaptation.
Implementation
import torch
import torch.nn as nn
class LoRALayer(nn.Module):
def __init__(
self,
in_features: int,
out_features: int,
rank: int = 4,
alpha: float = 1.0
):
super().__init__()
self.rank = rank
self.alpha = alpha
# Low-rank matrices
self.A = nn.Parameter(torch.zeros(rank, in_features))
self.B = nn.Parameter(torch.zeros(out_features, rank))
# Initialize A with Kaiming and B with zeros
nn.init.kaiming_uniform_(self.A, a=math.sqrt(5))
nn.init.zeros_(self.B)
# Scaling factor
self.scaling = alpha / rank
def forward(self, x: torch.Tensor) -> torch.Tensor:
# Compute low-rank adaptation: B @ A @ x
return (x @ self.A.T @ self.B.T) * self.scaling
Applying LoRA to a Linear Layer
class LinearWithLoRA(nn.Module):
def __init__(
self,
linear: nn.Linear,
rank: int = 4,
alpha: float = 1.0
):
super().__init__()
self.linear = linear
self.lora = LoRALayer(
in_features=linear.in_features,
out_features=linear.out_features,
rank=rank,
alpha=alpha
)
# Freeze the original weights
self.linear.weight.requires_grad = False
if self.linear.bias is not None:
self.linear.bias.requires_grad = False
def forward(self, x: torch.Tensor) -> torch.Tensor:
# Original output + LoRA adaptation
return self.linear(x) + self.lora(x)
Parameter Efficiency
For a weight matrix of size d × k:
- Full fine-tuning:
d × kparameters - LoRA with rank
r:r × (d + k)parameters
Example: For d = k = 4096 and r = 8:
- Full: 16,777,216 parameters
- LoRA: 65,536 parameters (0.39% of original)
DoRA: Weight-Decomposed Low-Rank Adaptation
The Innovation
DoRA extends LoRA by decomposing weights into magnitude and direction components, mimicking the nuanced adjustments observed in full fine-tuning.
Mathematical Formulation
DoRA decomposes the weight update as:
W' = m · (W₀ + BA) / ‖W₀ + BA‖_c
Where:
mis a learned magnitude vector (per output dimension)W₀ + BArepresents the directional component‖·‖_cdenotes column-wise normalization
Key Insight
Research shows that full fine-tuning makes subtle adjustments to both magnitude and direction, while standard LoRA primarily affects direction. DoRA’s decomposition allows for more expressive adaptations.
Implementation
class DoRALayer(nn.Module):
def __init__(
self,
in_features: int,
out_features: int,
rank: int = 4,
alpha: float = 1.0
):
super().__init__()
self.rank = rank
self.alpha = alpha
self.scaling = alpha / rank
# Low-rank matrices (same as LoRA)
self.A = nn.Parameter(torch.zeros(rank, in_features))
self.B = nn.Parameter(torch.zeros(out_features, rank))
# Learnable magnitude vector
self.m = nn.Parameter(torch.ones(out_features))
# Initialize
nn.init.kaiming_uniform_(self.A, a=math.sqrt(5))
nn.init.zeros_(self.B)
def forward(
self,
x: torch.Tensor,
base_weight: torch.Tensor
) -> torch.Tensor:
# Compute the adapted weight
lora_update = self.B @ self.A * self.scaling
adapted_weight = base_weight + lora_update
# Normalize column-wise (direction)
weight_norm = adapted_weight.norm(p=2, dim=1, keepdim=True)
direction = adapted_weight / (weight_norm + 1e-8)
# Apply magnitude scaling
final_weight = self.m.unsqueeze(1) * direction
return x @ final_weight.T
Applying DoRA to a Linear Layer
class LinearWithDoRA(nn.Module):
def __init__(
self,
linear: nn.Linear,
rank: int = 4,
alpha: float = 1.0
):
super().__init__()
self.linear = linear
self.dora = DoRALayer(
in_features=linear.in_features,
out_features=linear.out_features,
rank=rank,
alpha=alpha
)
# Initialize magnitude from pretrained weights
with torch.no_grad():
weight_norm = linear.weight.norm(p=2, dim=1)
self.dora.m.copy_(weight_norm)
# Freeze original weights
self.linear.weight.requires_grad = False
if self.linear.bias is not None:
self.linear.bias.requires_grad = False
def forward(self, x: torch.Tensor) -> torch.Tensor:
output = self.dora(x, self.linear.weight)
if self.linear.bias is not None:
output = output + self.linear.bias
return output
Magnitude Initialization
A crucial detail in DoRA is initializing the magnitude vector from the pretrained weights:
# Initialize m as the norm of each row of W₀
m_init = W₀.norm(p=2, dim=1)
This ensures the adapted weights start proportionally scaled to the original weights.
Comparison: LoRA vs DoRA
| Aspect | LoRA | DoRA |
|---|---|---|
| Parameters | r × (d + k) | r × (d + k) + d |
| Components | Direction only | Magnitude + Direction |
| Expressivity | Limited | Higher (mimics full FT) |
| Complexity | Simple | Slightly more complex |
| Performance | Good | Better on many tasks |
Usage with PEFT Library
For production use, Hugging Face’s PEFT library provides optimized implementations:
from peft import LoraConfig, get_peft_model, TaskType
# LoRA configuration
lora_config = LoraConfig(
task_type=TaskType.CAUSAL_LM,
r=8,
lora_alpha=32,
lora_dropout=0.1,
target_modules=["q_proj", "v_proj"]
)
# Apply to model
model = get_peft_model(base_model, lora_config)
# Check trainable parameters
model.print_trainable_parameters()
Project Structure
lora-dora-implementation/
├── dora_implementation/
│ ├── __init__.py
│ ├── lora.py # LoRA layer implementation
│ └── dora.py # DoRA layer implementation
├── notebooks/
│ └── demo.ipynb # Usage examples
├── config.py # Configuration settings
├── pyproject.toml # Poetry dependencies
└── README.md
Key Takeaways
- LoRA provides efficient fine-tuning by learning low-rank updates to frozen weights
- DoRA extends this by separating magnitude and direction components
- Both techniques dramatically reduce trainable parameters (often <1% of original)
- Understanding these implementations helps debug and customize PEFT strategies
References
- LoRA: Low-Rank Adaptation of Large Language Models - Hu et al., 2021
- DoRA: Weight-Decomposed Low-Rank Adaptation - Liu et al., 2024
- Sebastian Raschka’s LoRA from Scratch - Practical implementation guide
- Hugging Face PEFT Documentation